티스토리 뷰
위상 정렬이란?
꼭짓점 u와 v에서 꼭짓점 v까지의 모든 꼭짓점 u,v에 대해 u가 순서에서 v보다 먼저 오도록 꼭짓점을 선형 정렬하는 것이다
다시금 예를 들어, 그래프의 정점들을 수행할 작업의 순으로 나타낼 수 있고,
가장자리는 한 작업이 다른 작업보다 먼저 수행되어야 하는 제약 조건을 나타낼 수 있다.
여기서 위상 정렬은 비순환 그래프(DAG)인 경우에만 가능하다.
(비순환 그래프는 적어도 하나의 위상 순서를 가지며, 알고리즘은 선형 시간 내에 DAG의 위상 순서를 구성하는 것으로 알려져 있다.)
또한 DAG그래프만이 그래프에 사이클이 있으면서 두 정점 u,v가 사이클 속에 위치한 정점일 경우, 정점 u가 v보다 먼저 오거나 v가 u보다 먼저 올 수 있기에 DAG 그래프만 위상 정렬이 가능하다.
조금 어려운가?
그럼 예시를 두겠다.
네모2 세모2 하트2 총 6개 가 있다고 보자.네모를 다 배워야만 하트를 가질 수 있다고 한다면 네모 2는 무조건 하트 2 앞에 두는 조건 하에 정렬을 하면된다. < 이러한 조건이 위상정렬로 가능하다>

위와 같은 그래프를

아래로 표현 가능하게 하는 것이 위상 정렬이다.
그렇다면 어떤식으로 구현이 될까?

들어오는 에지가 없는 노드를 찾아보자
여기서 노드 A와 F에는 들어오는 에지가 없다!!
노드A를 소스 노드로 선택하고 이 노드를 모든 나가는 에지로 삭제한 후 결과 배열에 넣는다.

이제 노드 A의 나가는 에지를 삭제한 후 소스 노드의 인접 노드의 인도를 업데이트한다.
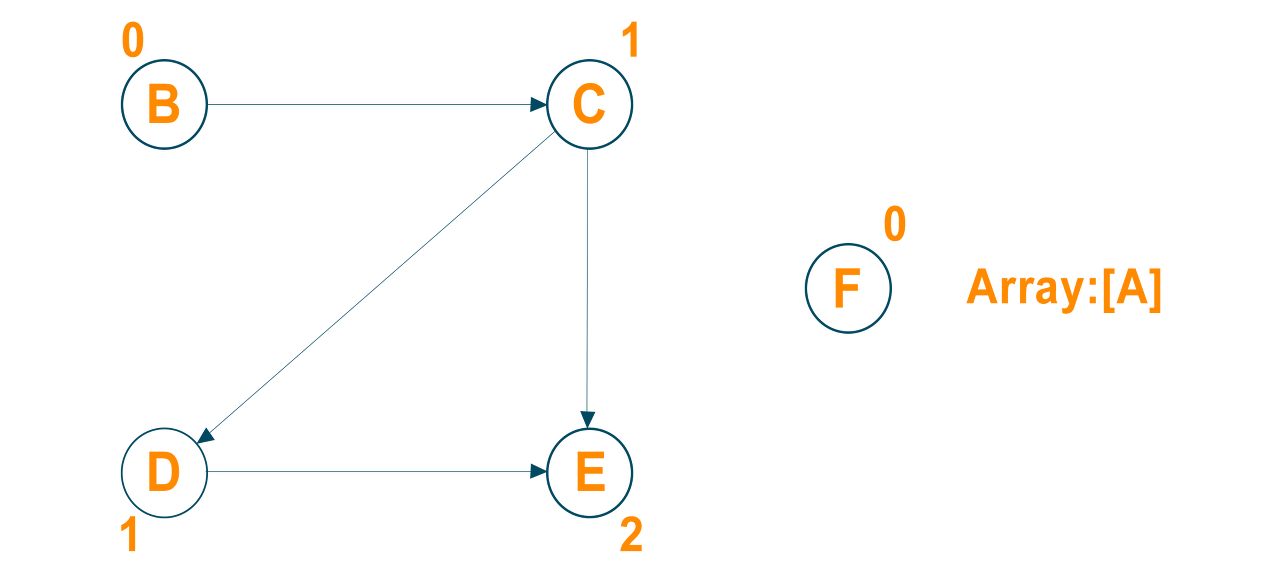
이제 0도 내의 노드와 나가는 에지를 다시 삭제하고 결과 배열에 삽입한다..
나중에 모든 인접 노드의 인도를 업데이트한다.

이제 위의 단계를 반복하여 아래와 같이 출력을 가지게된다.

두 번째 단계에서 소스 노드를 F로 선택했다면 그래프의 위상적인 종류는 F, A, B, C, D, E가 될 것이다.
따라서 모든 방향 비순환 그래프에 대해 둘 이상의 위상 정렬이 가능하다.
다음은 코드를 통해 이해해보자.
2623번: 음악프로그램
첫째 줄에는 가수의 수 N과 보조 PD의 수 M이 주어진다. 가수는 번호 1, 2,…,N 으로 표시한다. 둘째 줄부터 각 보조 PD가 정한 순서들이 한 줄에 하나씩 나온다. 각 줄의 맨 앞에는 보조 PD가 담당한
www.acmicpc.net
import sys
from collections import deque
def topology_sort():
result = []
q = deque()
for i in range(n):
if indegree[i] == 0:
q.append(i)
while q:
now = q.popleft()
result.append(now + 1)
for i in graph[now]:
indegree[i] -= 1
if indegree[i] == 0:
q.append(i)
if sum(indegree) > 0:
print(0)
else:
[print(i) for i in result]
n, m = map(int, sys.stdin.readline().split())
indegree = [0] * n
result = [1] * n
graph = [[] for i in range(n)]
for _ in range(m):
list_ = list(map(int, sys.stdin.readline().split()))
for a, b in zip(list_[1:], list_[2:]):
graph[a - 1].append(b - 1)
indegree[b - 1] += 1
topology_sort()'Algorithm Theory' 카테고리의 다른 글
| 크루스칼 알고리즘(Kruskal's algorithm) (0) | 2022.07.10 |
|---|---|
| 플로이드 와샬 알고리즘(Floyd-Warshall Algorithm) (0) | 2022.07.10 |
| 벨만 포드 알고리즘(Bellman-Ford Algorithm) (0) | 2022.07.10 |
| 다익스트라 알고리즘(Dijkstra's Algorithm) (0) | 2022.07.10 |
| 투 포인터(Two Pointers Algorithm) (0) | 2022.07.10 |
